Answer:
Option C Both gift boxes have the same length for a given volume
Explanation:
step 1
David's gift box
Calculate the side length of the box for a given volume
we have
![f(x)=\sqrt[3]{x-1}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/oc3zjus8weh346fnzsjnbwabvv4r6yrqmd.png)
For
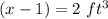 ------>
------>
![f(x)=\sqrt[3]{2}=1.26\ ft](https://img.qammunity.org/2020/formulas/mathematics/middle-school/qdt9abfjx5tqsy4b1vcd5vwa0cf0esiaqv.png)
For
 ------>
------>
![f(x)=\sqrt[3]{4}=1.59\ ft](https://img.qammunity.org/2020/formulas/mathematics/middle-school/2r69iz0mgevqxi61se69u5j0ngjf0ee5um.png)
For
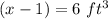 ------>
------>
![f(x)=\sqrt[3]{6}=1.82\ ft](https://img.qammunity.org/2020/formulas/mathematics/middle-school/1yq3anqb7ja8l4xsymbwj1qonsjaaz4dh8.png)
For
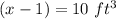 ------>
------>
![f(x)=\sqrt[3]{10}=2.15\ ft](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ukuq7xl5jrhfwa0ogbha630yh92pmc4hkz.png)
therefore
Both gift boxes have the same length for a given volume