Question

HELP!!!!

Iron (III) oxide reacts with solid carbon in the followed reaction: 2Fe2O3(s) + 3C(s) → 4Fe(s) + 3CO2(g) What mass of Fe2O3 is necessary to produce 100. L of CO2 at 300. K and 2.10 atm? 823 g Fe2O3 908 g Fe2O3 1,110 g Fe2O3 1,360 g Fe2O3

Answer 1

908 g Fe₂O₃

General Formulas and Concepts:

Chemistry - Gas Laws

Combined Gas Law: PV = nRT

• P is pressure
• V is volume (in liters)
• n is number of moles
• R is a constant -
  `0.0821 (L \cdot atm)/(mol \cdot K)`
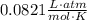
• T is temperature (in Kelvins)

Chemistry - Stoichiometry

• Reading a Periodic Table
• Using Dimensional Analysis

Step-by-step explanation:

Step 1: Define

[RxN] 2Fe₂O₃ (s) + 3C (s) → 4Fe (s) + 3CO₂ (g)

[Given] 100 L CO₂ at 300 K and 2.10 atm

Step 2: Find Moles

Apply the Combined Gas Law and solve.

`(2.10 \ atm)(100 \ L) = n(0.0821 (L \cdot atm)/(mol \cdot K) )(300 \ K)\\((2.10 \ atm)(100 \ L))/((0.0821 (L \cdot atm)/(mol \cdot K) )(300 \ K)) = n\\n = 8.52619 \ mol \ CO_2`

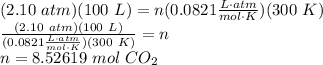
Step 3: Identify Conversions

[RxN] 3 mol CO₂ = 2 mol Fe₂O₃

Molar Mass of Fe - 55.85 g/mol

Molar Mass of O - 16.00 g/mol

Molar Mass of Fe₂O₃ - 2(55.85) + 3(16.00) = 159.7 g/mol

Step 4: Stoichiometry

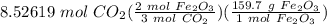`8.52619 \ mol \ CO_2((2 \ mol \ Fe_2O_3)/(3 \ mol \ CO_2) )((159.7 \ g \ Fe_2O_3)/(1 \ mol \ Fe_2O_3) )` = 907.755 g Fe₂O₃

Step 5: Check

We are given 3 sig figs. Follow sig fig rules and round.

907.755 g Fe₂O₃ ≈ 908 g Fe₂O₃