(4 * 3^x)' Evaluate

Question

`(4 * 3^x)'`

Evaluate

Answer 1

`\approx 4.39 \cdot 3^x`

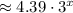
Explanation:

Recall a property:

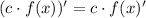`(c\cdot f(x))'=c\cdot f(x)'`, where
`c` is a constant.

Apply the property to the task:

`(4\cdot 3^(x))'=4\cdot (3^x)'`

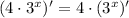
Recall a property of the derivative of an exponential function:

`(a^x)'=a^x \cdot ln(a)`

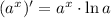
Apply the property to the task:

`4\cdot 3^x \cdot \ln 3`

Since
`\ln 3\approx 1.0986`, it follows:

`4\cdot 3^x \cdot \ln 3 \approx 4\cdot 1.0986 \cdot \ln3`

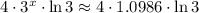
Multiply the numbers.

The answer is about
`4.39\cdot 3^x`.