Answer:
The sum of the given series is 1023
Explanation:
Geometric series states that a series in which a constant ratio is obtained by multiplying the previous term.
Sum of the geometric series is given by:

where a is the first term and n is the number of term.
Given the series:

This is a geometric series with common ratio(r) = 2
We have to find the sum of the series for 10th term.
⇒ n = 10 and a = 1
then;
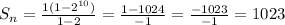
Therefore, the sum of the given series is 1023