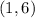Question

Write the quadratic function f(x) = 3x2 - 6x + 9 in vertex form. A) f(x) = 3(x - 3)2 + 9 B) f(x) = 3(x - 1)2 + 6 C) f(x) = 3(x + 3)2 + 6 D) f(x) = 3(x + 1)2 + 9

Answer 1

Option B
`f(x)=3(x-1)^(2)+6`

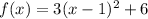
Explanation:

we have

`f(x)=3x^(2) -6x+9`

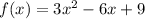
Group terms that contain the same variable, and move the constant to the opposite side of the equation

`f(x)-9=3x^(2) -6x`

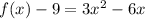
Factor the leading coefficient

`f(x)-9=3(x^(2) -2x)`

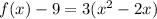
Complete the square. Remember to balance the equation by adding the same constants to each side

`f(x)-9+3=3(x^(2) -2x+1)`

`f(x)-6=3(x^(2) -2x+1)`

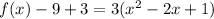
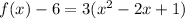
Rewrite as perfect squares

`f(x)-6=3(x-1)^(2)`

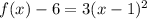
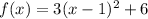`f(x)=3(x-1)^(2)+6` ------> equation in vertex form

the vertex is the point
`(1,6)`