Question

Steel loading ramps are used to load a lawn mower onto a truck bed 37.5 inches above the ground. If the ramp make a 30° angle with the ground, find the length of the ramps in feet

Answer 1

The answer is 75 inches

Explanation:

We see that the figure will relate the sides hypotenuse and perpendicular. So using trigonometric functions

Sin ( 30 ) = Perp / hyp

Sin (30) = 37.5 / hyp

0.5 = 37.5 / hyp

hyp = 37.5 / 0.5

hyp = 75 inches

Answer 2

6.25 feet.

Explanation:

Please find the attachment.

Let L be the length of the ramp in feet.

We have been given that steel loading ramps are used to load a lawn mower onto a truck bed 37.5 inches above the ground. The ramp make a 30° angle with the ground.

We can see from our attachment that ramp and truck bed forms a right triangle with ground. The truck bed is opposite side and length of ramp is hypotenuse of our given angle.

Since we know that Sine relates the opposite and hypotenuse of a right triangle, so we will use Sine to solve for L.

`\text{Sine}=\frac{\text{Opposite}}{\text{Hypotenuse}}`

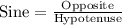
Upon substituting our given values in above formula we will get,

`\text{Sin(30)}=(37.5)/(L)`

`L=\frac{37.5}{\text{Sin(30)}}`

`L=(37.5)/(0.5)`

`L=75`

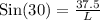
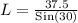
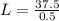
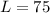
Therefore, the length of the ramp is 75 inches.

Let us convert the length of ramp in feet.

1 feet = 12 inches.

`\text{75 inches}=\frac{75\text{ inches}}{\frac{12\text{ inches}}{\text{feet}}}`

`\text{75 inches}=\frac{75\text{ inches}}{12}* \frac{\text{ feet}}{\text{inches}}`

`\text{75 inches}=(75)/(12)*\text{ feet}`

`\text{75 inches}=6.25\text{ feet}`

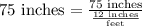
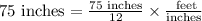
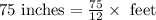
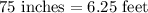
Therefore, the length of the ramp is 6.25 feet.