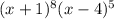Answer:
30
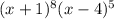
Explanation
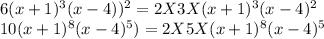
In order to find the Least common multiple we write each of the factor only once from each of the expression and for the common expression we take their LCM as maximum of the exponent in all expressions
as here in the question exponent of (x+1) are 3 and 8 so we take exponent 8
likewise for (x-4) we shall take maximum of 2 and 5 which is 5
so our expression for Least common multiple will be
2X3X5 X
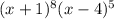
30