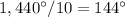Answer:
Part a) The sum of the interior angle measures of a regular decagon is
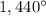
Part b) The measure of each interior angle of a regular decagon is
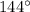
Explanation:
Part a)
we know that
The sum of the interior angles of a polygon is equal to

where
n is the number of sides of a polygon
In this problem
 ----> regular decagon
----> regular decagon
substitute
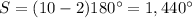
Part b) What is the measure of each interior angle of a regular decagon?
If the figure is a regular polygon, then all interior angles are equal
so
Divide the sum of the interior angles by the number of sides