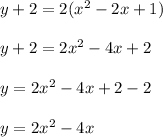Answer:
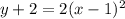 -----> vertex form
-----> vertex form
 -----> standard form
-----> standard form
Explanation:
we know that
The equation of a vertical parabola in vertex form is equal to
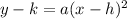
where
(h,k) is the vertex of the parabola
In this problem we have


substitute the values and solve for a
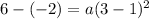
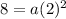
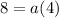
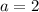
the equation in vertex form is equal to
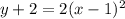
Find the equation of the parabola in standard form
we know that
the equation of the parabola in standard form is equal to
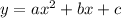
we have
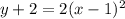
convert to standard form