Help Please! What is the simplest form of the product? ^3 sqrt 4x^2 * ^3 sqrt 8x^7

Question

asked Jul 27, 2020 202k views

2 Answers

Muny · Answer 1 · 2020-08-01T16:59:15+0000

Answer:

$2x^3\sqrt[3]{4}$

Explanation:

We have been given an expression
$\sqrt[3]{4x^2} *\sqrt[3]{8x^7}$ and we are asked to find the product of our given expression.

Using exponent rule of power to powers
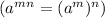(a^(mn)=(a^m)^n) we can write
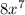8x^7 as
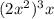(2x^2)^3x and
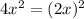4x^2=(2x)^2 .

Upon substituting these values in our expression we will get,

$\sqrt[3]{4x^2} *\sqrt[3]{(2x^2)^3x}$

Using exponent rule
$\sqrt[n]{x^m} =x^{(m)/(n)}$ we will get,

$\sqrt[3]{4x^2} *2x^2\sqrt[3]{x}$

Multiplying
$\sqrt[3]{x}$ by
$\sqrt[3]{4x^2}$ we will get,

$\sqrt[3]{4x^3} *2x^2$

Using exponent rule
$\sqrt[n]{x^m} =x^{(m)/(n)}$ we will get,

$x\sqrt[3]{4}*2x^2$

$x*2x^2\sqrt[3]{4}$

$2x^3\sqrt[3]{4}$

Therefore, the simplest form of the product of our given expression will be
$2x^3\sqrt[3]{4}$ .