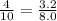Question

What proportional segment lengths verify that BC¯¯¯¯¯∥DE¯¯¯¯¯ ? Fill in the boxes to correctly complete the proportion. $$ = $$ A triangle with vertices labeled as A, B, C. Side B C is base. Sides A B and A C contain midpoints D and E, respectively. A line segment is drawn from D to E. Side A D is labeled as 4. Side D B is labeled as 6. Side A E is labeled as 3.2. Side E C is labeled as 4.8.

Answer 1

`(4)/(10)=(3.2)/(8.0)`

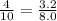
Explanation:

Given,

ABC is a triangle,

In which, AD = 4 unit, DB = 6 unit, AE = 3.2 unit and EC = 4.8 unit,

⇒
`(AD)/(AB)=(4)/(4+6)=(4)/(10)=0.4`

`(AE)/(EC)=(3.2)/(3.2+4.8)=(3.2)/(8)=0.4`

`\implies (AD)/(AB)=(AE)/(EC)`

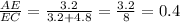
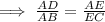
⇒ Δ ADE ≅ Δ ABC

⇒ ∠ADE ≅ ∠ABC and ∠AED ≅ ∠ACB

By the converse of alternate interior angle theorem.

BC ║ DE

Hence, the required proportion of segment is,

`(4)/(10)=(3.2)/(8.0)`