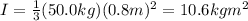A) 42.7 kg m^2
We can consider Olga has a uniform rod, rotating about one of her end, with her mass distributed along the body. Therefore, her moment of inertia is given by
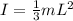
where
m = 50.0 kg is the mass
L = 1.6 m is the length of Olga's body
Substituting into the equation, we find
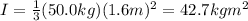
B) 10.6 kg m^2
The problem is the same as before, however this time the length of Olga's body is just half the length she had before:
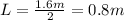
Therefore, her moment of inertia will be