Answer:
y =
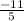 x +
x +

Explanation:
Linear function is defined by y = ax+b
where a and b are constants and (x,y ) are variables given as point
using point (3,2) that is plugging x =3 and y =2 ,we
2 = 3a+b ............. equation(1)
likewise using point (-2,13) and plugging x =-2 and y =13 ,we get
13 = -2a+b .......... equation(2)
Solving the equation (1) and 2

subtracting equation 2 from equation 1
3a+b = 2
-2a+b = 13
__-_______________
we have 5a = -11
a=
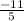
plugging a=
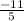 in equation (1),we get
in equation (1),we get
3(
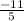 ) +b =2
) +b =2
b = 2 -3(
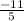 )
)
b = 2+
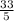
b=

therefore equation is obtained by plugging
a =
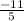 and b =
and b =

we get equation as
y =
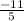 x +
x +
