Answer:
Option A is correct.
Explanation:
Common Ratio of Geometric series is obtained by dividing by each next term of the series to its previous term
here in the problem two consecutive terms are -1 and -i
so dividing -i by -1 in order to find common ratio
r =
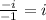
Since here common ratio is i
next 3 terms are given by

Therefore common ratio is i and next three terms are 1,i and -1
Therefore option A is correct .