Question

Fabiano wants to score at least 6 . 5 6.5 points in a major chess tournament. He scores 1 1 point for each game that he wins, and he scores 0 . 5 0.5 points for each game that ends in a draw. Write an inequality that represents the number of games Fabiano should win ( W ) (W) and draw ( D ) (D) to achieve his goal.

Answer 1

`W+0.5D\geq 6.5`

Explanation:

Let W represent the number of games Fabiano should win and D represent the number games of Fabiano should draw.

We have been given that Fabiano scores 1 point for each game that he wins, so points scored in W games will be 1W=W.

We are also told that he scores 0.5 points for each game that ends in a draw. So points scored in D games will 0.5D.

As Fabiano wants to score at least 6.5 points in a major chess tournament, so total number of points scored in W games and D games should be greater than or equal to 6.5.

We can represent this information in an inequality as:

`W+0.5D\geq 6.5`

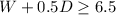
Therefore, the inequality
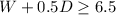`W+0.5D\geq 6.5` represents the number of games Fabiano should win and draw to achieve his goal.