Question

If a≠0, b≠0, c≠0 and a+b+c=0, then prove that a²/bc +b²/ca +c²/ab =3

the / represents a fraction

Answer 1

see explanation

Explanation:

Express the left side as a single fraction with abc as the common denominator

`(a^2)/(bc)` +
`(b^2)/(ca)` +
`(c^2)/(ab)`

=
`(a^3+b^3+c^3)/(abc)`

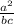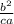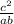
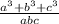
[ a³ + b³ + c³ = (a + b + c)(a² + b² + c² - ab - bc - ac ) + 3abc ]

since a + b + c = 0 then

(a + b + c)(a² + b² + c² - ab - bc - ac) = 0 , hence

a³ + b³ + c³ = 3abc

------------------------------------------------

=
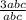`(3abc)/(abc)` = 3