Answer:
Length of AC is 13.19 cm
Explanation:
We have the right triangle ADB with an angle 65° and the length of hypotenuse = 7 cm.
As we know, 'In a right angled triangle, the angles and sides can be written in trigonometric forms'.
That is,
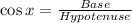
i.e.
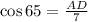
i.e
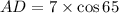
i.e

i.e. AD = 3 cm
Also, Pythagoras Theorem' states that 'The sum of squares of the length of the sides in a right triangle is equal to the square of the length of the hypotenuse'.
That is,
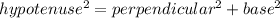
i.e.
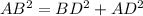
i.e.
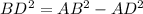
i.e.
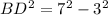
i.e.
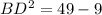
i.e.

i.e.
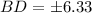
Since, length of a side cannot be negative.
So, BD = 6.33 cm
Again using Pythagoras Theorem for the right triangle BDC, we have,
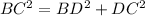
i.e.

i.e.
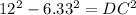
i.e.
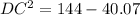
i.e.
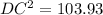
i.e.
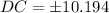
Since, length of a side cannot be negative.
So, DC = 10.194 cm.
Finally, as the side AC is the sum of segments AD and DC, we have,
AC = AD + DC
i.e. AC = 3 + 10.194
i.e. AC = 13.19 cm
Hence, the length of AC is 13.19 cm.