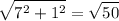Question

Consider the vectors u = <-4, 7> and v = <11, -6>. u + v = < , > ||u + v|| ≈ units

Answer 1

5
`√(2)`

Explanation:

u + v = < - 4, 7 > + < 11, - 6 > = < - 4 + 11, 7 - 6 > = < 7, 1 >

| u + v | =
`√(7^2+1^2)` =
`√(50)` = 5
`√(2)`

Answer 2

If U = <-4, 7> , V = <11, -6> are vectors in R²:

* U + V = <7, 1>

* |U + V| =
`√(50)`

Explanation:

1. Let's define first, the sum operation between vectors U and V in R²:

*
`$U = <u_(x),u_(y)> V = <v_(x),v_(y)>$`

⇒
`$U + V = <u_(x) + v_(x), u_(y) + v_(y) >$`

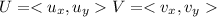
Where:

`$u_(x) , v_(x)$` are U and V x coordinates and
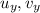`$u_(y) , v_(y)$` are U and V y coordinates.

In this example:

`$U = <-4,7> V = <11,-6}> => U + V = <7, 1>$`

2. Let’s define secondly, length operator of a vector U in R²:

*
`$U = <u_(x),u_(y)>$`

⇒ |U|=
`$ \sqrt{u_(x)^2 + u_(y)^2}$`

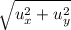
In this example:

U + V is also a vector in R²

⇒ |U + V|=
`$ \sqrt{(u_(x) +v_(x)) ^2 + (u_(y) +v_(y)) ^2}$`

⇒ |U + V|=
`$ √(7 ^2 + 1 ^2) = √(50) $`