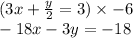Question

Consider this system: 3x + 1/2y = 3 6x - y = 2 Which of the following operations would eliminate the x-terms if the two equations were added together afterward? Multiply the first equation by –6.

Multiply the first equation by –2.


Multiply the first equation by 2.


Multiply the first equation by 6.



use elimination to solve the system

Answer 1

`x = (2)/(3), y = 2`

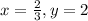
Explanation:

We are b:

`3x + (y)/(2) = 3\\6x - y = 2`

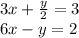
We need to eliminate x from the above two equations so that we can find the value of y and then the value of x.

In order to eliminate x we multiply first equation by -2 and add both the equations to solve for y.

This can be shown as:

`(3x + (y)/(2) = 3)* (-2) = -6x - y = -6\\6x - y = 2`

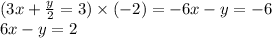
Now we add these two equations

`(-6x - y) + (6x -y) = (-6) + (2)\\-2y = -4\\\Rightarrow y = 2`

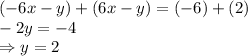
Now putting value of y in equation, we get

`6x -2 = 2\\6x = 4\\\Rightarrow x = (2)/(3)`

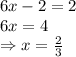
Now, we have to multiply the first equation by -6

`(3x + (y)/(2) = 3)* -6\\ -18x - 3y = -18`

Answer 2

The correct answer is multiply the first equation by -2.

Explanation:

The reason for this is then you'd be left with the following two equations.

-6x - y = -6

6x - y = 2

If you add these two together you would cancel out the x terms.