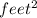Question

Mr. Crow, the head groundskeeper at High Tech Middle School, mows the lawn along the side of the gym. The lawn is rectangular, and the length is 5 feet more than twice the width. The perimeter of the lawn is 250 feet. Homework Help ✎

Use the 5-D Process to find the dimensions of the lawn.

Use the dimensions you calculated in part (a) to find the area of the lawn.

What are the answers and how do i solve it thank you

Answer 1

Dimensions, Length = 85 feet and Width = 40 feet

Area of lawn = 3400
`feet^2`

Explanation:

Given: Lawn is rectangular in shape

Length of lawn is 5 feet more than twice its breath/width

Perimeter of Lawn = 250 feet

To find: (a) Length and width of lawn

(b) Area of Lawn

First let the a variable for width/breadth. Say, Width = b.

So, the length of lawn = 2b + 5

Perimeter of Rectangle = 2 × ( length + width )

Now, substitue given values in this formula

∴ Perimeter of Lawn = 2 × ( 2b + 5 + b )

`250 = 2*{(2b+b+5)}\\250= 2*{(3b+5)}\\3b+5 = (250)/(2)\\3b = 125 -5\\3b = 120\\b=(120)/(3)\\b=40`

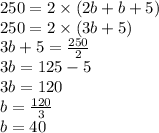
∴width = 40 feet

⇒ length = 85 feet

Now we find are of lawn using formula of area of rectangle

Area of lawn = length × width

= 85 × 40

= 3400
`feet^2`

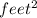
Dimensions, Length = 85 feet and Width = 40 feet

Area of lawn = 3400
`feet^2`