Question

A six-foot-tall person is standing next to a flagpole. The person is casting a shadow 1 1/2 feet in length, while the flagpole is casting a shadow 5 feet. How tall is the flagpole?

Answer 1

20

Explanation:

First, your answer should look like this: 6/1.5 X/5

Now your gonna wanna cross multiply 6 and 5 then put X and 1.5 like this 1.5x

After that, your question should look like this: 1.5x=30

Now divide 30 by 1.5 and you should get 20

X=20

Remember this: height/shadow

Hoped this helps!

Answer 2

Answer: 20 ft

This problem can be solved by the Thales’s theorem, which states:

Two triangles are similar when they have equal angles and proportional sides

It should be noted that to apply Thales' Theorem, it is necessary to establish the two triangles are similar, that is, that they have the corresponding angles equal or that their sides are proportional to each other.

Now, if we measure the shadow of the flagpole and the shadow of the person, at the same moment, we can use the first Thales' Theorem to calculate the height of the flagpole, knowing the height of the person.

In this case we have two similar triangles (Figure attached) where
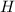`H` is the height of the flagpole,
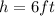`h=6 ft` is the height of the person,
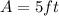`A=5 ft` is the length of the shadow of the flagpole and
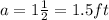`a=1(1)/(2)=1.5 ft` is the length of the shadow of the person.

Having this clear, we can write the following relation with both similar triangles:

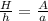`(H)/(h)=(A)/(a)` (1)

We know all these lengths except
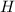`H`, which is the value we want to to find.

So, in order to approach this problem we have to find
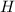`H` from equation (1):

`H=(A)/(a)h`

`H=(5 ft)/(1.5 ft)(6 ft)`

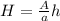
Then:

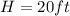`H=20 ft` >>>>>This is the height of the flagpole