Question

As part of your retirement plan, you want to set up an annuity in which a regular payment of $35,000 is made at the end of each year. You need to determine how much money must be deposited earning 6% compounded annually in order to make the annuity payment for 20 years. a. $391,125.87 c. $397,502.32 b. $395,083.12 d. $401,447.24

Answer 1

Option d)$401,447.24

Explanation:

We are given that as part of your retirement plan, you want to set up an annuity in which a regular payment of $35,000 is made at the end of each year at rate of 6% compounded annually for 20 years

So first of all we need to find the future value of annuity using the formula as shown below :

`FV= p([(1+(r)/(n))^((n)(t))-1)])/((r)/(n))`

Here, FV = future value of annuity

p = $35000 (annual deposit)

r is rate = 6% = 0.06

n = number of compounding = 1 ( as we are compounding annually )

t = number of years = 20

So plugging in all the values in the formula , we get

`FV= 35000([(1+(0.06)/(1))^((1)(20))-1)])/((0.06)/(1))`

Simplifying further , we get

`FV= 35000([(1+0.06)^(20)-1)])/(0.06)`

Plugging in the given values in the calculator , we get

FV = $ 1287495.69

So far we have got the Total amount for annuity , from here we need to use the concept of compound interest and find the principal amount to be deposited to get the required total amount of $ 1287495.69

The formula for compound interest when compounded annually is given by:

`A=P(1+r)^t`

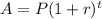
Here A = 1287495.69 (Total amount required)

P = ( principal amount to be deposited to meet the required total amount )

r = 6% = 0.06

t = 20

So plugging in all the known values in the formula , we get

`1287495.69= P(1+0.06)^(20)`

simplifying further, we get

`(1287495.69)/((1.06)^(20))= P`

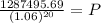
so required amount to be deposited is given by :

P = $401,447.24

Hope it was helpful !:)