Question

For a class picnic two teachers went to the same store to purchase drinks. One teacher purchased 18 juice boxes and 32 bottles of water and spent $22.30. The other teacher purchased 14 juice boxes and 26 bottles of water, and spent $17.90

Answer 1

a) The system of equations that represents this situation is:

18j+32w=22.30 (1)

14j+26w=17.90 (2)

This is a system with two equations and two unknown quantities, which are j and w.

b) If we want to prove Kara is wrong with the prices, we have to substitute the prices she gave for each juice box and each bottle of water (j=0.52 and w=0.33) in the system of equations.

Note that the term "cents" refers to a quantity divided by 100, that is why we are using 0.52 and 0.33.

Using equation (1):

18(0.52)+32(0.33)=19.92

`19.92\\eq22.30`

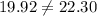
Using equation (2):

14(0.52)+26(0.33)=15.86

`15.86\\eq17.90`

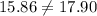
c) Now we have to solve the system of equations to find the actual cost of each item:

Isolating j from (1):

`18j=22.30-32w`

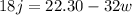
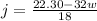`j=(22.30-32w)/(18)` (3)

Substituting (3) in (2) and isolating w:

`14((22.30-32w)/(18))+26w=17.90`

`(7)/(9)(22.30)-(7)/(9)(32w)+26w=17.90`

`(7)/(9)(22.30)-17.90=(7)/(9)(32w)-26w`

`w=(-0.55)/(-1.11)`

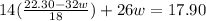
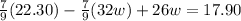
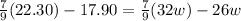
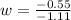
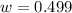`w=0.499` (4) >>>>>This is the cost of each bottle of water

Now, substituting (4) in (1):

`18j+32(0.4999)=22.30`

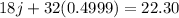
and finding j:

`18j=22.30-15.968`

`j=(6.332)/(18)`

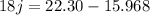
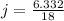
Then:

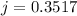`j=0.3517` >>>>>This is the cost of each juice box

Finally, each juice box costs $0.3517 and each bottle of water costs $0.499