Question

PLEASE HELP.

For each recursively defined sequence below write the first few terms. Then use the terms to write an explicit equation.


a1 = 17

an+1 = an – 3


a1 = 20

an+1 = 1/2 · an

Answer 1

1. Terms are 17, 14, 11, 8, 5,...... and explicit equation is
`a_(n)=17-3(n-1)`.

2. Terms are 20, 10, 5, 2.5, 1.25,...... and explicit equation is
`a_(n)=20* ((1)/(2))^(n-1)`.

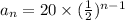Explanation:

Ques 1: We are given the recursive formula for the sequence as,

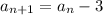`a_(n+1)=a_(n)-3`, where
`a_(1)=17`.

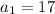So, substituting the values of 'n' from {1,2,3,.....}, we get,

`a_(2)=a_(1+1)=a_(1)-3=17-3=14`

`a_(3)=a_(2+1)=a_(2)-3=14-3=11`

`a_(4)=a_(3+1)=a_(3)-3=11-3=8`

`a_(5)=a_(4+1)=a_(4)-3=8-3=5`

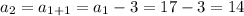
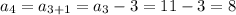
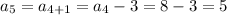
Thus, the sequence is given by 17, 14, 11, 8, 5,......

As, the explicit equation of an arithmetic sequence is of the form,
`a_(n)=a_(1)+d(n-1)`, where
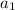`a_(1)` is the first term and 'd' is the common difference.

As, the common difference, d = 14 - 17 = -3

Thus, we get,

The given sequence has the explicit equation,
`a_(n)=17-3(n-1)`.

Ques 2: We are given the recursive formula for the sequence as,

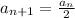`a_(n+1)=(a_(n))/(2)`, where
`a_(1)=20`.

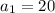So, substituting the values of 'n' from {1,2,3,.....}, we get,

`a_(2)=a_(1+1)=(a_(1))/(2)=(20)/(2)=10`

`a_(3)=a_(2+1)=(a_(2))/(2)=(10)/(2)=5`

`a_(4)=a_(3+1)=(a_(3))/(2)=(5)/(2)=2.5`

`a_(5)=a_(4+1)=(a_(4))/(2)=(2.5)/(2)=1.25`

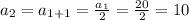
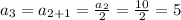
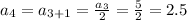
Thus, the sequence is given by 20, 10, 5, 2.5, 1.25,......

As, the explicit equation of a geometric sequence is of the form,
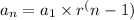`a_(n)=a_(1)* r^(n-1)`, where
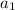`a_(1)` is the first term and 'r' is the common ratio.

As, the common ratio,
`r=(10)/(20)=(1)/(2)`

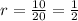
Thus, we get,

The given sequence has the explicit equation,
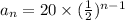`a_(n)=20* ((1)/(2))^(n-1)`.

Answer 2

Explicit formula for

1)
`a_n=17-3(n-1)`

2)
`a_n=((1)/(2) )^(n-1)\cdot 20`

Explanation:

W have to find the first few terms of the given sequence and then find an explicit equation

Explicit formula = f(n) + d(n-1) , where,

f(n) is first term,

d is common difference,

n-1 is one term less than the term number.

1)

Given :
`a_1=17\\\\a_(n+1)=a_n-3`

`\text{We put n =1, we get,}\\\\a_2=a_1-3=17-3=11=17-3(2-1)\\\\\\\text{We put n =2, we get,}\\\\\\a_3=a_2-3=11-3=8=17-3-3=17-3\cdot 2=17-3(3-1)\\\\\text{We put n =3, we get,}\\\\\\a_4=a_3-3=8-3=5=17-3-3-3=17-3\cdot 3=17-3(4-1)\\`

Thus, we obtained an explicit formula,

`a_n=17-3(n-1)`

2)

Given :
`a_1=20\\\\a_(n+1)=(1)/(2) \cdot a_n`

`\text{We put n =1, we get,}\\\\a_2=a_1-3=17-3=11=17-3(2-1)\\\\\\\text{We put n =2, we get,}\\\\\\a_3=a_2-3=11-3=8=17-3-3=17-3\cdot 2=17-3(3-1)\\\\\text{We put n =3, we get,}\\\\\\a_4=a_3-3=8-3=5=17-3-3-3=17-3\cdot 3=17-3(4-1)\\`

Thus, we obtained an explicit formula,

`a_n=17-3(n-1)`

`\text{We put n =1, we get,}\\\\\\a_2=(1)/(2) \cdot a_1=(1)/(2) \cdot 20=10=((1)/(2) )^(2-1)\cdot 20\\\\\\\text{We put n =3, we get,}\\\\\\a_4=(1)/(2) \cdot a_3=(1)/(2) \cdot 5=(5)/(2)=((1)/(2) )^(4-1)\cdot 20\\\\\\`

Thus, we obtained an explicit formula,

`a_n=((1)/(2) )^(n-1)\cdot 20`