Question

Can someone please help me?

Find the roots using Synthetic Division.


`x^(4) -7x^(3) +13x^(2) +3x-18`

I know that there are 4 roots. But I need help finding the factors of the last term and the first term and finding possible rational roots.

Answer 1

now, let's recall the rational root test, check your textbook on it.

so p = 18 and q = 1

so all possible roots will come from the factors of ±p/q

now, to make it a bit short, the factors are loosely, ±3, ±2, ±9, ±1, ±6.

recall that, a root will give us a remainder of 0.

let us use +3.

`\bf x^4-7x^3+13x^2+3x-18 \\\\[-0.35em] ~\dotfill\\\\ \begin{array}rrrrr 3&1&-7&13&3&18\\ &&3&-12&3&18\\ \cline{1-6} &1&-4&1&6&0 \end{array}\qquad \implies (x-3)(x^3-4x^2+x+6)`

well, that one worked... now, using the rational root test, our p = 6, q = 1.

so the factors from ±p/q are ±3, ±2, ±1

let's use 3 again

`\bf \begin{array}r 3&1&4&1&6\\ &&3&-3&-6\\ \cline{1-5} &1&-1&-2&0 \end{array}\qquad \implies (x-3)(x-3)(x^2-x-2)`

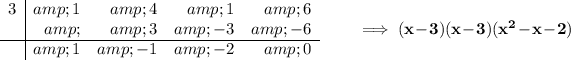
and of course, we can factor x²-x-2 to (x-2)(x+1).

(x-3)(x-3)(x-2)(x+1).