Question

Hello, everyone!

Here is the problem I am stuck with.:
Based on the “National Ambient Air Quality Objectives”, the acceptable hourly average concentration of carbon monoxide (CO) is 35 mg/m^3.

Find the acceptable concentration of CO in ppm if the temperature is -30 °C and pressure is 0.92 atm. Express the concentration as a percent by volume.

Could someone please help me understand how to do it?

Any input would be greatly appreciated!

Answer 1

Answer: 27.09 ppm and 0.003 %.

First, for air pollutants, ppm refers to parts of steam or gas per million parts of contaminated air, which can be expressed as cm³ / m³. Therefore, we must find the volume of CO that represents 35 mg of this gas at a temperature of -30 ° C and a pressure of 0.92 atm.

Note: we consider 35 mg since this is the acceptable hourly average concentration of CO per cubic meter m³ of contaminated air established in the "National Ambient Air Quality Objectives". The volume of these 35 mg of gas will change according to the atmospheric conditions in which they are.

So, according to the law of ideal gases,

PV = nRT

where P, V, n and T are the pressure, volume, moles and temperature of the gas in question while R is the constant gas (0.082057 atm L / mol K)

The moles of CO will be,

n = 35 mg x
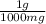`(1 g)/(1000 mg)` x
`(1 mol)/(28.01 g)`

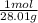
→ n = 0.00125 mol

We clear V from the equation and substitute P = 0.92 atm and

T = -30 ° C + 273.15 K = 243.15 K

V =
`(0.00125 mol x 0.082057 (atm L)/(mol K)  x 243 K)/(0.92 atm)`

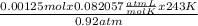
→ V = 0.0271 L

As 1000 cm³ = 1 L then,

V = 0.0271 L x
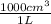`(1000 cm^(3) )/(1 L)` = 27.09 cm³

Then the acceptable concentration c of CO in ppm is,

c = 27 cm³ / m³ = 27 ppm

To express this concentration in percent by volume we must consider that 1 000 000 cm³ = 1 m³ to convert 27.09 cm³ in m³ and multiply the result by 100%:

c = 27.09
`(cm^(3) )/(m^(3) )` x
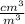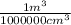`(1 m^(3) )/(1 000 000 cm^(3) )` x 100%

c = 0.003 %

So, the acceptable concentration of CO if the temperature is -30 °C and pressure is 0.92 atm in ppm and as a percent by volume is 27.09 ppm and 0.003 %.