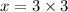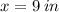ANSWER
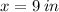
EXPLANATION
The volume of a rectangular prism is given by the formula,

We substitute the dimensions to obtain,
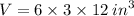
The volume of the rectangular pyramid is,

Equating the two volumes gives,

We divide through by 6×12 to get,
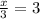
We solve for x to obtain,