Answer:
Part 1)

Part 2)

Part 3)
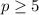
Part 4)
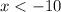
Part 5)
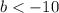
Part 6)
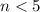
Part 7)
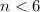
Part 8)
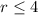
Part 9)
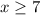
Part 10)
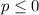
Part 11)
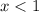
Part 12)

Explanation:
Part 1)
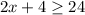
Subtract 4 both sides
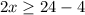
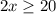
Divide by 2 both sides

the solution is the interval ------> [10,∞)
The solution is the shaded area to the right of the solid line at number 10 (closed circle).
see the attached figure
Part 2)
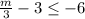
Adds 3 both sides
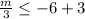
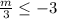
Multiply by 3 both sides

the solution is the interval ------> (-∞,-9]
The solution is the shaded area to the left of the solid line at number -9 (closed circle).
see the attached figure
Part 3)

applying the distributive property left side
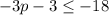
adds 3 both sides
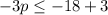
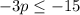
Multiply by -1 both sides
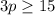
Divide by 3 both sides
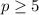
the solution is the interval ------> [5,∞)
The solution is the shaded area to the right of the solid line at number 5 (closed circle).
see the attached figure
Part 4)
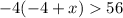
applying the distributive property left side
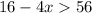
Subtract 16 both sides
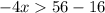
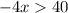
Multiply by -1 both sides
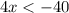
Divide by 4 both sides
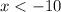
the solution is the interval ------> (-∞,-10)
The solution is the shaded area to the left of the dashed line at number -10 (open circle).
see the attached figure
Part 5)
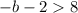
adds 2 both sides
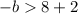
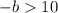
Multiply by -1 both sides
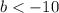
the solution is the interval ------> (-∞,-10)
The solution is the shaded area to the left of the dashed line at number -10 (open circle).
Part 6)
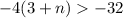
applying the distributive property left side
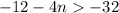
adds 12 both sides
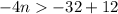
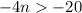
multiply by -1 both sides
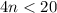
divide by 4 both sides
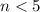
the solution is the interval ------> (-∞,5)
The solution is the shaded area to the left of the dashed line at number 5 (open circle).
see the attached figure
Part 7)

Subtract 4 both sides
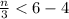
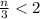
Multiply by 3 both sides
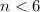
the solution is the interval ------> (-∞,6)
The solution is the shaded area to the left of the dashed line at number 6 (open circle).
see the attached figure
Part 8)
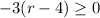
applying the distributive property left side
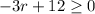
subtract 12 both sides

divide by -1 both sides
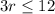
divide by 3 both sides
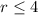
the solution is the interval ------> (-∞,4]
The solution is the shaded area to the left of the solid line at number 4 (closed circle).
see the attached figure
Part 9)
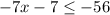
Adds 7 both sides

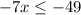
Multiply by -1 both sides
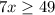
Divide by 7 both sides
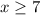
the solution is the interval ------> [7,∞)
The solution is the shaded area to the right of the solid line at number 7 (closed circle).
see the attached figure
Part 10)
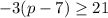
applying the distributive property left side
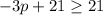
subtract 21 both sides
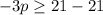
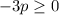
Multiply by -1 both sides
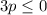
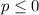
the solution is the interval ------> (-∞,0]
The solution is the shaded area to the left of the solid line at number 0 (closed circle).
see the attached figure
Part 11)
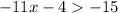
Adds 4 both sides
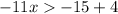

Multiply by -1 both sides
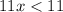
Divide by 11 both sides
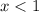
the solution is the interval ------> (-∞,1)
The solution is the shaded area to the left of the dashed line at number 1 (open circle).
see the attached figure
Part 12)
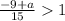
Multiply by 15 both sides
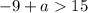
Adds 9 both sides
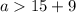

the solution is the interval ------> (24,∞)
The solution is the shaded area to the right of the dashed line at number 24 (open circle).
see the attached figure