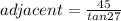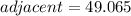Question

The sun is behind a building and casting a shadow. How long is the shadow if the building is 25 feet tall and the angle, of the shadow, opposite the building is 27°?

Answer 1

ANSWER

The length of the shadow is 49 ft to nearest feet.

Step-by-step explanation

We can find the length of the shadow using the tangent ratio.

Recall that,


`\tan(27 \degree) = (opposite)/(adjacent)`
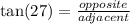
From the diagram, the length of the shadow is the side of the triangle that is adjacent to the 27° angle


`\tan(27 \degree) = (45)/(adjacent)`

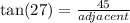
This implies that,


`adjacent = (45)/(tan27 \degree)`


`adjacent = 49 .065`