Question

A cannonball is launched from the ground at an angle of 30 degrees above the horizontal and a speed of 30 m/s. Ideally (no air resistance) the ball will land on the ground with a speed of

Answer 1

When ball hits the ground its velocity will be 30 m /sec

Step-by-step explanation:

We have given that there is no air resistance

So from energy conservation initial energy will be equal to final energy

So
`U_I+KE_I=U_F+KE_F`

As the ball is initially at the ground and finally also on the ground

So
`U_I=U_F=0`

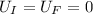
As we know that mass is also conserved

So initial velocity will be equal to final velocity

So when ball hit the ground its velocity will be 30 m /sec

Answer 2

As we know that here no air resistance while ball is moving in air

So here we will say that

initial total energy = final total energy

`KE_i + U_i = KE_f + U_f`

here we know that

`Ui = U_f = 0` (as it will be on ground at initial and final position)

so we will say

`KE_i = KE_f`

since mass is always conserved

so we will say that final speed of the ball must be equal to the initial speed of the ball

so we have

`v_f = v_i = 30 m/s`