Question

.

Find the exponential function that satifies the given conditions:
Initial value = 62, decreasing at a rate of 0.47% per week.


f(t) = 62 ⋅ 0.9953t

f(t) = 62 ⋅ 1.47t

f(t) = 62 ⋅ 1.0047t

f(t) = 0.47 ⋅ 0.38t

Answer 1

Option first is the correct answer

Explanation:

Equation for the exponential function is given by

`A= P(1-r)^t`

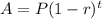
where A is amount after t time

P = initial amount

r = rate of interest

If it is decreasing by rate of r%

Here in the question initial value is given to be 62 therefore P = 62

and rate of decreasing is 0.47% which can be written as 0.0047 in decimal form

`f(t) = 62(1-0.0047)^t`

f(t) = 62
`(0.9953)^t`

Is the exponential function that satisfies the condition

therefore option first is the correct answer,

Answer 2

f(t) = 62 ⋅ 0.9953t

Explanation:

The function decreases at a rate of 0.47%

That will mean, the initial value decreases by 0.47?

100% - 0.47% = 99.53%

The next value will be 99.53% of the initial value.

∴ 99.53% × 62 = 0.9953 × 62.

After a time t, the value will be:

0.9953t × 62

∴ Answer = 62 × 0.9953