Question

A 5.0-kg bag of groceries is tossed onto a table at 2.0 m/s and slides to a stop in 1.6 s .

Modify the equation FΔt=Δ (mv) to find the force of friction.

Express your answer to two significant figures and include the appropriate units.

Answer 1

-6.3 N

Step-by-step explanation:

The equation we need to use is:

`F \Delta t = \Delta (mv)`

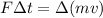
where

F is the force of friction, that slows down the bag

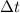`\Delta t` is the time of the motion

m is the mass of the bag

v is the speed of the bag

Since the mass of the bag does not change, we can rewrite the equation as

`F \Delta t= m \Delta v`

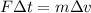
where we have:

`\Delta t=1.6 s\\m=5.0 kg\\\Delta v=-2.0 m/s`

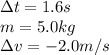
Substituting and re-arranging the equation, we can find the force of friction:

`F=(m\Delta v)/(\Delta t)=((5.0 kg)(-2.0 m/s))/(1.6 s)=-6.3 N`

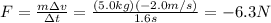
where the negative sign means that the force is in the opposite direction to the motion of the bag.