Question

Choose the graph which matches the function. (2 points)
f(x) = 3x-1

Answer 1

Observe the attached image

Explanation:

We know that
`f(x) = 3^(x-1)` is an exponential function, therefore its graph must have the form that corresponds to this type of functions.

The first thing to do is find the cut points of the function.

Cut point with the y axis:

`x = 0\\\\y = 3^(0-1)\\\\y = 3^(-1)\\\\y = (1)/(3)`

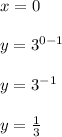
The function cuts the y-axis on
`y = (1)/(3)`

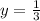
Cutting point with the x axis:

`y = 0\\\\0 = 3^(x-1)`

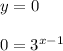
To clear x we must apply log on both sides of the equality, but the log(0) is not defined. Then, the function does not cut to the x axis.

The graph that represents the function f(x) is the one that cuts in
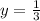`y = (1)/(3)` and does not cut the x-axis