Question

1. What is (f⋅g)(x)?

f(x)=x^4−9

g(x)=x^3+9



Enter your answer in the box.



2. What is (f−g)(x)?



f(x)=x^3−2x^2+12x−6

g(x)=4x^2−6x+4



Enter your answer in the box.

Answer 1

(f⋅g)(x)
`= x^7 + 9x^4 - 9x^3 -81`

`(f - g)(x) = x^3 - 6x^2 + 18x + 6x - 10`

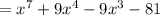
Explanation:

For the first part of the question we have two functions

`f(x) = x^4 -9`

`g(x) = x^3 + 9`

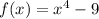
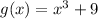
If the expression refers to the multiplication of f and g, then:

(f⋅g)(x)
`= f (x)g(x)`

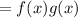
So we multiply the function f(x) with the function g(x)

(f⋅g)(x)
`= (x^4 - 9)(x^3 + 9)`

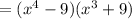
(f⋅g)(x)
`= x^7 + 9x^4 - 9x^3 -81`

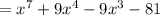
For the second part we have the functions:

`f(x) = x^3 -2x^2 + 12x - 6\\\\g(x) = 4x^2 - 6x + 4`

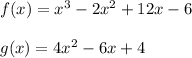
We wish to find (f - g) (x). We know that

`(f - g)(x) = f(x) - g(x)\\\\(f - g)(x) = x^3 - 2x^2 + 12x - 6 - [4x^2 - 6x + 4]\\\\(f - g)(x) = x^3 - 2x^2 + 12x - 6 -4x^2 + 6x - 4`

`(f - g)(x) = x^3 - 6x^2 + 18x + 6x - 10`