Question

If 3^2x+1 = 3^x+5, what is the value of x? 2 3 4 6

Answer 1

Choice C is the answer.

Explanation:

We have given a equation.

`3^(2x+1) =3^(x+5)`

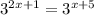
We have to find the value of x.

We use following property to solve this question.

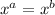`x^(a) =x^(b)`⇒ a = b

`3^(2x+1) =3^(x+5)`

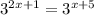
Using above property,we get

2x+1 = x+5

Adding -x to both sides of above equation,we get

-x+2x+1 = -x+x+5

x+1 = 5

Adding -1 to both sides of above equation,we get

x+1-1 = 5-1

x = 4 which is the answer.

Answer 2

Answer: 4

Explanation:

Here the given expression is,

`3^(2x+1)= 3^(x+5)`

We can write,

`3^(2x+1)= 3^(x+5)\implies 2x+1=x+5` (Because
`a^m=a^n \implies m = n` )

⇒
`2x+1-x =5` ( Subtracting x on both sides)

⇒
`x = 5-1` ( Subtracting 1 on both sides)

⇒
`x=4`

⇒ Fourth Option is correct.