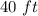Answer:
 by
by
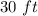
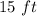 by
by
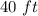
Explanation:
In this problem I'm assuming the office is rectangular.
so
The area of rectangle is equal to

where
L is the length of the rectangle
W is the width of the rectangle
In this problem we have

so
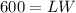 ------> equation A
------> equation A
Find two possible dimensions of the office
case A) Assume a length side L and find the value of W in the equation A
so
For
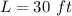
substitute in the equation and solve for W
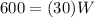

The dimensions are
 by
by
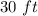
case B) Assume a length side L and find the value of W in the equation A
so
For
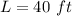
substitute in the equation and solve for W
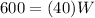
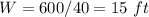
The dimensions are
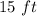 by
by