Question

In Lesson 3.05 we discussed comparing the key features of two functions given in different forms. Given the functions below:

a) Compare the y-intercepts of f(x) and g(x). Use complete sentences.

b) Compare the vertical asymptotes of f(x) and g(x). Use complete sentences.

Answer 1

try desmos or ask the teacher

Answer 2

A. f(x):
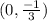`(0,(-1)/(3))`, g(x): (0,0)

B. f(x): 'y= 0' as horizontal asymptote, g(x): 'x= 4' as vertical asymptote.

Explanation:

We are given the functions,
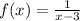`f(x)=(1)/(x-3)` and graph of g(x).

Part A: We know that,

'Y-intercepts are the points where the graph of the function crosses y-axis'.

That is, 'y-intercept is obtained when x= 0'.

So, we have,

When x= 0,
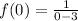`f(0)=(1)/(0-3)` i.e.
`f(0)=(-1)/(3)`.

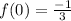Thus, the y-intercept of function f(x) is the point
`(0,(-1)/(3))`.

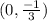Also, from the graph of g(x), we see that, the graph crosses y-axis at the point (0,0).

Thus, the y-intercept of g(x) is (0,0).

Part B: We know that,

'Asymptotes are the line or curves approaching the graphs of the functions arbitrarily close'.

Now, as we have the function f(x) is a rational function and the degree of numerator is less than the degree of the denominator.

So, the function f(x) will have 'y= 0' as the horizontal asymptote.

Also, from the graph of the function g(x), we see that,

The line 'x= 4' is the vertical asymptote as it is approaching the graph closely.

So, the function g(x) have 'x= 4' as the vertical asymptote.