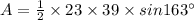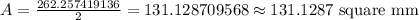Answer: 131.1287 square mm (approx)
Explanation:
The area of a triangle,

Where
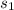 and
and
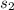 are adjacent sides and
are adjacent sides and
 is the include angle of these sides,
is the include angle of these sides,
Here PR and QR are adjacent sides and ∠R is the included angle of these sides,
Thus, we can write,
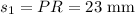 ,
,
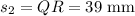 and
and
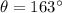 ,
,
Thus, the area of the triangle PQR,