Question

Which of the following is a valid exclusion for the algebraic fraction 8ab^2x/4a^2b-8ab^2

(the up arrow means that the following number is an exponent)

a) a ≠ 0, b ≠ 0
b) a ≠ 0, b ≠ 0, a ≠ b
c) b ≠ 0, a ≠ b
d) a ≠ 0, b ≠ 0, a ≠ 2b

Answer 1

Option (d) is a valid exclusion for the given algebraic fraction

(d) a ≠ 0, b ≠ 0, a ≠ 2b

Explanation:

Given algebraic expression
`(8ab^2x)/(4a^2b-8ab^2)`

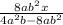
We have to find the conditions which is valid exclusion for the algebraic fraction
`(8ab^2x)/(4a^2b-8ab^2)`.

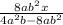Consider , the given algebraic expression ,

`(8ab^2x)/(4a^2b-8ab^2)`

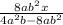
We first solve the given fraction in simplest form ,

Taking 4ab common from denominator, we get,

`(8ab^2x)/(4ab(a-2b))`

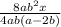
Solving the fraction , we get,

`(2bx)/((a-2b))`

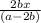
For the above fraction to be valid denominator has to be non zero, that is

`a-2b\\eq 0\\\\\\ \Rightarrow a\\eq 2b`

Thus, option (d) is a valid exclusion for the given algebraic fraction