Answer:
(3,2),(3,-2),(-3,2),(-3,-2)
Explanation:
The given system of equations is
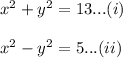
Add equations (i) and (ii) is
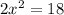
Solve the equation for x. For this divide both sides by 2
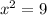
Take square root both sides
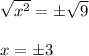
For x = 3, -3

Therefore, the solutions are
(3,2),(3,-2),(-3,2),(-3,-2)
Therefore, all the points are the solutions of the system of equations.