Question

Determine if the series is convergent or divergent -5+25-125+....

a) convergent
b) divergent

Answer 1

b)Divergent

Explanation:

Given is a series

-5+25-125+....

We find that this is following a pattern such that each term is multiplied by -5 to get the next term

In other words, this series is a geometric series with common ratio r =-5 and I term a=-5

Since sum of n terms of geometric series =
`(a(r^n-1))/(r-1) =\frac{-5{(-5)^n-1}}{-5-1}`

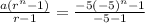
Since |r|=|-5|>1, we find that this sum tends to infinity or -infinity as n tends to infinity

In other words, the series diverges