Question

Determine the common ratio and find the next three terms of the geometric sequence

Answer 1

BBBBBBBBBBBBBBBBBBBBBBBBBB

Explanation:

Answer 2

Option (b) is correct.

The three terms of the GP are
`12,12√(2),24` with common ratio
`√(2)`

Explanation:

Consider the given geometric sequence
`3√(2),6,6√(2)......`

Geometric sequence is a sequence of numbers where each term is find by multiplying the previous one by a fixed number called the common ratio (r).

`a,\ ar,\ ar^(2),\ ar^(3),\ ar^(4),\ \ldots`

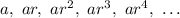
Consider the first two terms of the given GP.

`a=3√(2),ar=6` thus r can be find by dividing ar by a,

thus the common ratio is
`r=(6)/(3√(2))=√(2)`

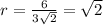
Now we have to find the next three terms of GP . so multiply r in given last term to obtain next three terms , we get ,

`6√(2) * √(2)=6* 2= 12 \\\\\\12 * √(2)= 12√(2)\\\\\\\12√(2) *√(2)=24`

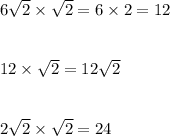
Thus, the three terms of the GP are
`12,12√(2),24` with common ratio
`√(2)`.

Option (b) is correct.