Answer:
B.
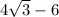
Explanation:
We have,
The first term of the series,
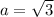 .
.
The common difference is given by,
 i.e.
i.e.
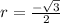 .
.
Since, the given series is an infinite series, then,
Sum of an infinite series =
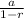
i.e. Sum the series =
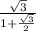
i.e. Sum the series =

i.e. Sum the series =
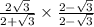
i.e. Sum the series =
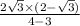
i.e. Sum the series =
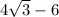
Thus, the sum of the series is
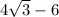 .
.