Question

The product of (a + b)(a − b) is a2 − b2. (1 point) Sometimes Always Never

Answer 1

The product of
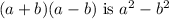`(a + b)(a-b)\ \text{is}\ a^2-b^2` is always true.

Explanation:

Given : A statement that the product of
`(a + b)(a-b)\ \text{is}\ a^2-b^2`.

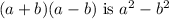We have to check that above statement is always true, sometimes or never.

Let us take some values for a and b and then check whether the left hand side is equal to right hand side,

Let a = 3 and b = 2

Then left side ⇒ (a + b) (a - b) = (3 + 2) (3 - 2) = (5)(1) = 5

Also Right side ⇒
`a^2-b^2=(3)^2-(2)^2=9-4=5`.

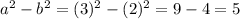Since, LHS = RHS ,

Thus, the product of
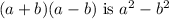`(a + b)(a-b)\ \text{is}\ a^2-b^2` is always true.

Answer 2

ANSWER


`\boxed{Always}`
EXPLANATION


The given product is


`( a - b)(a + b)`

This is always equal to


`{a}^(2) - {b}^(2)`


The identity


`( a - b)(a + b) = {a}^(2) - {b}^(2)`


is called difference of two squares.


We can verify this by simply expanding the brackets using the distributive property to obtain,



`( a - b)(a + b) = a(a + b) - b(a + b)`




`( a - b)(a + b) = {a}^(2) + ab - ab- {b}^(2)`

This simplifies to


`( a - b)(a + b) = {a}^(2) - {b}^(2)`