Question

What is the 8th term of the geometric sequence a2 = 20 and r = 5

Answer 1

8th term of geometric sequence is 312500

Explanation:

Given :
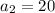`a_2=20` and common ratio (r) = 5

We have to find the 8th term of the geometric sequence whose
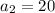`a_2=20` and common ratio (r) = 5

Geometric sequence is a sequence of numbers in which next term is found by multiplying by a constant called the common ratio (r).

`a_n=ar^(n-1)` ......(1)

where
`a_n` is nth term and a is first term.

For given sequence

a can be find using
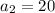`a_2=20` and r = 5

Substitute in (1) , we get,

`a_2=ar^(2-1)`

`\Rightarrow 20=a(5)`

`\Rightarrow a=4`

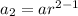
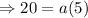
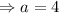
Thus, 8th term of the sequence denoted as
`a_8`

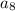
Substitute n= 8 in (1) , we get,

`a_8=ar^(8-1) \\\\a_8=(4)r_(7) \\\\a_8=4(5)^7=4 * 78125=312500`

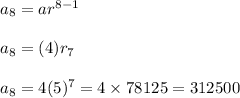
Thus 8th term of geometric sequence is 312500