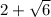Answer:
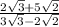 is equal to
is equal to
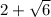
Explanation:
Consider the given fraction,
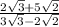
We are required to rational denominator,
Multiply and divide numerator by
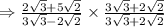 , we get,
, we get,
Using identity ,
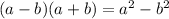 in denominator, we get,
in denominator, we get,
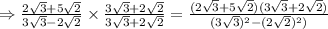
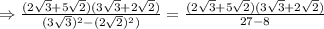
On solving further , we get,
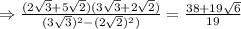
solving , we get,
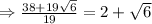
Thus,
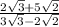 is equal to
is equal to