Question

Given: △ACM, m∠C=90°, CP ⊥ AM
AC:CM=3:4, MP-AP=1. Find AM.

Answer 1

Explanation:

It is given that in △ACM, m∠C=90°, CP ⊥ AM

, AC:CM=3:4, MP-AP=1.

Let AC=3x and CM=4x, then from △ACM, we get

`(AM)^2=(AC)^2+(CM)^2`

`(AM)^2=(3x)^2+(4x)^2`

`(AM)^2=25x^2`

`AM=5x`

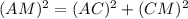
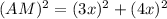
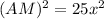
Now, AM=MP+AP⇒5x=MP+AP (1)

It is also given that MP-AP=1 (2)

Therefore, from (1) and (2),

(MP+AP)(MP-AP)=5x

`(MP)^2-(AP)^2=5x`

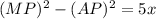
Add and subtract
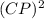`(CP)^2` on the left side,

`(MP)^2+(CP)^2-(CP)^2-(AP)^2=5x`

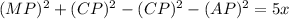
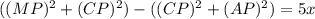`((MP)^2+(CP)^2)-((CP)^2+(AP)^2)=5x` (3)

But, since CP ⊥ AM, Δ CMP and Δ CAP are right triangles. Therefore,

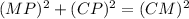`(MP)^2+(CP)^2=(CM)^2` and

`(CP)^2+(AP)^2=(AC)^2`

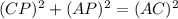
Thus, Equation (3) becomes,

`(CM)^2-(AC)^2=5x`

`(4x)^2-(3x)^2=5x`

`7x^2=5x`

`x=(5)/(7)`

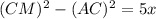
Therefore, AM=5x

`AM=5((5)/(7))=(25)/(7)`.