Question

find a positive angle less than one revolution around the unit circle that is co-terminal with the given angle -15pi/17

Answer 1

ANSWER

`=(19)/(17) \pi`

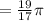
Step-by-step explanation

To find a positive angle that is coterminal with

`- (15)/(17) \pi`

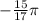
We add multiples of 2π until we get a positive angle that is less than one revolution,


We add to obtain,



`- (15)/(17) \pi + 2\pi`


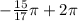
This simplifies to,


`= (19)/(17) \pi`

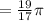
This is the first positive angle that is coterminal with

`- (15)/(17) \pi`


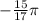
and is less than one revolution.