Answer:
We have the equation,
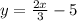
i.e.
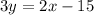
i.e.
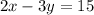
It is required to find a system of equations having infinite solutions.
We know that,
'When the equations are dependent or their graphs are same, the system of equations has infinite number of solutions'.
So, we can take any equation having same graph as that of
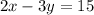 .
.
Let, us take
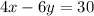
So, from the graph of these equations below, we get the system of equations having infinite solutions as,
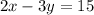 and
and
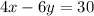 .
.