Question

What is the value of x? Enter your answer in the box. x = ​​ A triangle with vertices labeled as A, B, and C. Side B C is the base. A line segment is drawn from A to base B C that bisects angle B A C into two parts marked with single arcs. Side A B is labeled as 9. Side A C is labeled as 15. Side B C is divided into two equal parts labeled as 2 x minus 1 and 3 x.

Answer 1

x = 5

Explanation:

For better explanation of the solution, see the attached diagram of the problem :

The triangle angle bisector theorem states that the line which bisects an angle of a triangle divides the opposite two sides of the triangle in two equal segment which are proportional to the other two sides of the triangle.

Now, from the diagram : AD is the angle bisector angle B

`\implies(AB)/(AC)=(BD)/(CD)\\\\\implies (9)/(15) = ((2x-1))/((3x))`

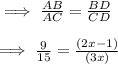
On Cross multiplication :

⇒ 9 × 3x = 15 × (2x - 1)

Using the distributive property,

⇒ 27x = 15×2x - 15×1

⇒ 27x = 30x - 15

Subtract 30x from each side:

⇒ 27x - 30x = 30x - 15 - 30x

⇒ -3x = -15

⇒ x = 5